Homework problems
Last additions posted at 2.30 pm, Saturday.
Let’s consider the Edgeworth box for Catherine and Henry.
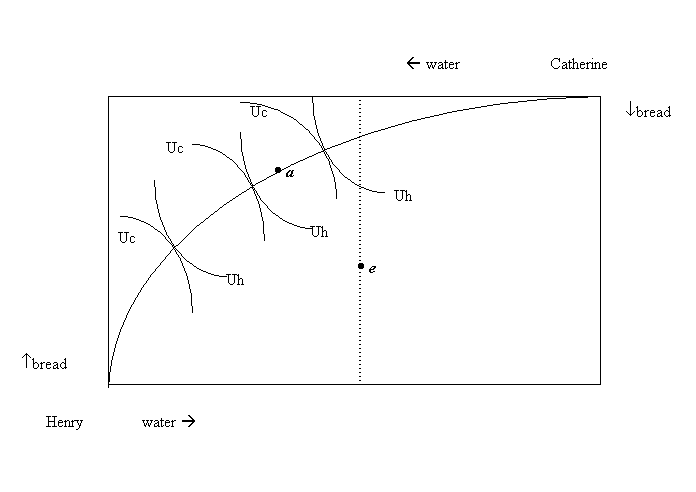

Uh and Uc are some indifference curves for Henry and Catherine. Diagonal curve is the contract curve that shows all the Pareto-optimal allocations of bread and water between them. If the water is distributed equally then the allocation is going to lie on the dotted vertical line that corresponds to all equal allocations of water. The actual location of this point depends on the Henry’s and Catherine’s endowments of bread. For example, if they also have equal amounts of bread, the allocation is at point e. This is not an efficient allocation. If they could trade bread for water they could end up somewhere on the contract curve, for example at point a. There exists, of course, a chance that equal allocation is optimal: it is when the endowments of bread are such that the allocation point lies at the intersection of the contract curve and the dotted line, but the probability is negligible and the guys can reach it through exchange anyway, if they want.
Lesson: Equal distribution by government is in general inefficient.
Ch.3. #4.
If the social utility function is W = UL + UA, then the social indifference curves are straight lines with the slope of -1. You can find this in a straightforward manner following the definition of indifference curve: location of all points that yield the same value of the utility function (in our case social utility function W). Let’s try finding some indifference curve for some level of social utility, say 1. We write W = UL + UA = 1. Rearranging the terms obtains:
UL
= 1 – UA
This is the algebraic form for this indifference curve. Geometrically, it’s a straight line with the slope -1. By the same procedure, we can construct indifference curves fro other levels of the social utility: UL = 2 – UA for W=2, UL = 3 – UA for W=3, etc. They are all parallel straight lines.
This social utility function implies that the society views Augustus and Livia as “interchangeable” members of society: equal distribution of goods that produces UL = UA = 1 and W=2 is as good as the situation, when Livia is starving to death (UL = 0) and Augustus is twice better off then before (UA = 2). The total is the same W=2. (What a cruel world!)
If the social utility function is W = UL + 2UA, then the society values Augustus’ utility twice as much as Livia’s utility. Note that this society still does care about who gets what: UA = 0 and UL = 3 produce the same social outcome as, say, UA = 1 and UL = 1.
The limited productive possibilities of the society produce the utility possibility frontier (UPF) that shows the maximum of what one can have given that the other member of the society gets specific level of the utility. The socially optimal point is where UPF is tangent to the highest reachable social indifference curve. Part (c) of the problems specifies a fancy UPF. If the social utility is like the first one of the above, W = UL + UA, then the optimal point is O1. If it is W = UL + 2UA, then the optimal point is O2.


Lesson: Two societies with identical resources (as expressed by UPFs) can favor significantly different patterns of distribution, depending on the social preferences (the shape of the social utility function, W).
Additional problem from Hwk #1.
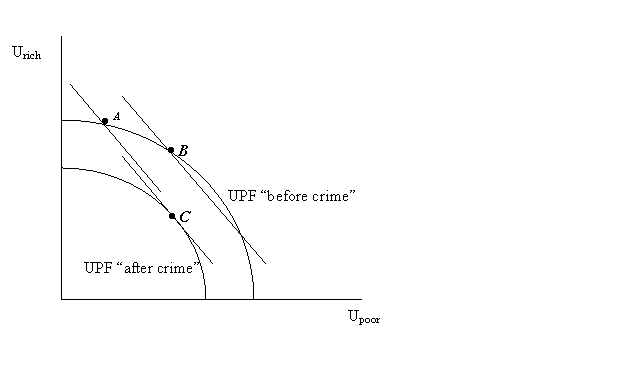
If someone poor is stealing something from someone rich, does this increase social utility (welfare)? Seems like the answer is yes. If the society values utility of everyone and the utility is subject to diminishing returns, then the rich guy loses less (in the utility of stolen valuables) then the poor criminal gains. The society is better off: it moves from point A to pint B in the diagram below. However, every crime results typically in additional costs (damage) to the victim and/or the society as a whole. We can represent this effect in a diagram by shrinking UPF, so that the actual move is not from A to B but to C. This makes the society worse off.
By the same logic, charity looks like a simple transfer that increases social welfare but is unlikely to increase Pareto-effciency. (You an show this in an Edgeworth box.) However, this is not true. In fact, there are positive externalities involve, for example, reduction of crime rate and – see above - reduction of losses from crime. UPF moves outward. The overall result can be increase in utility levels for both the giver and the beneficiary. This is a Pareto-improvement.

When considering whether a certain good or service should be provided publicly or privately we must consider the following.
a) Does this good have the properties of a pure public good - nonrival in consumption and nonexcludable, where nonexcludable means that it is too expensive to maintain a system that collects payments for access to the good.
b) Are there any positive or negative externalities involved? These lead to insufficient or excessive, respectively, levels of production of the good from the social perspective.
c) Can a competitive market exist for this good? (Remember that the First theorem of welfare economics shows that if certain things are true then markets produce efficient outcomes without government intervention. In particular, perfectly competitive market for the good exist.)
All things considered highways should be provided publicly, although they are not pure public goods. Note that fees charged for the use of toll roads do not make the latter private goods. User fee ideally serve the purpose of directing consumers (motorists) with relatively low preferences for highways (low demand for fast transportation) to alternative routes. This reduces congestion of the highway (i.e. prevents devaluation of this good for the users). If everyone has identical demand for the good then user fee is nothing more than a special-purpose tax.
Ch.5, #2
The case of a private good with positive externality. Cassanova is throwing parties for his own pleasure, but his friends (guests) get additional benefit without paying anything. Marginal benefit for Cassanova’s numerous friends is constant: MBf = b. Marginal benefit for Cassanova is diminishing (diminishing utility) – he is getting bored. Marginal social benefit is the sum of both MSB = MBc + MBf = MBc + b. Cassanova chooses optimal number of parties so as to equalize marginal benefits and marginal costs: MBc = MC. The result is Np (subscript p stands for privately optimal decision). The optimal number of parties for the society equates MSB and MC; the socially optimal number is Ns.
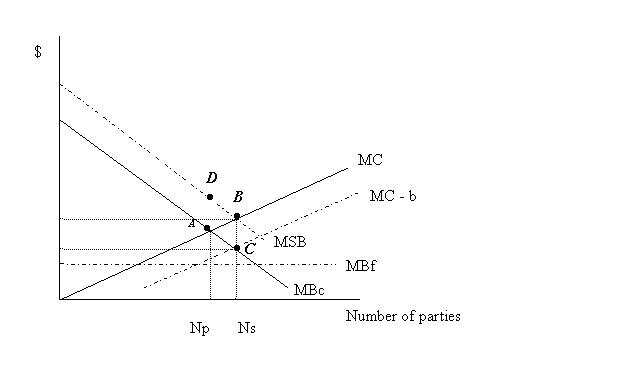

To induce Cassanova to throw Ns parties, the government should pay him a subsidy b that covers the difference between marginal costs and his (private) marginal benefit at Ns. This measure reduce his costs – shifts MC downward by b. Now it is optimal for him to provide Ns parties.
The outcomes in terms of surplus are the following: Cassanova’s net loss from privately unoptimal number of parties is measured by the triangle ABC (the costs exceed benefits here) but he is paid total subsidy Ns * b by the government, which obviously exceeds his loss. Cassanova’s friends gain (Ns – Np) * b. These are their benefits from additional parties.
The question is, of course, what does it cost for the government to raise funds needed to pay the subsidy. If we assume that these costs are zero, then the subsidy is a net transfer from the government to Cassanova and the net social gain is triangle ADB – due to the increase of party “output” to the socially optimal level.
The main lesson from this problem is that you need to play the whole cycle of majority voting in order to find out, whether it yields any result. Double-peaked preferences make the decision-making by majority voting problematic, but they do not necessarily make the solution impossible.
Consensus is certainly more difficult to achieve than to make a decision by majority voting. A good thing about consensus is that it can produce only Pareto-efficient (and therefore socially improving) results: nothing than hurts anyone is going to be adopted. This is not true for majority voting.
The small
community of
Ch.8. #1
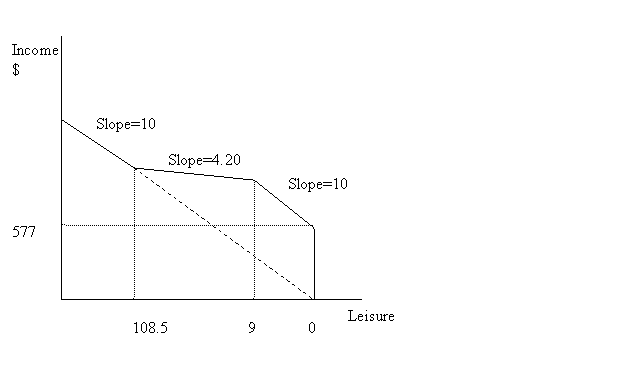
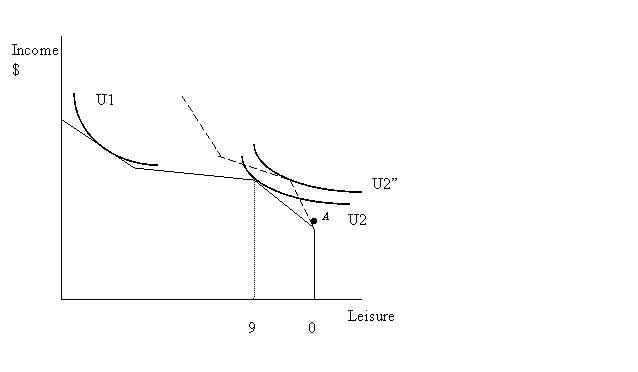
Elizabeth’s budget constraint consists of 4 chunks: 1) vertical bar at 0 our work (all leisure) with the height of $577 – base benefits; 2) first 9 hours of work with the slope of 10 (her wage is $10 per hour); 3) after 9 hours, her income exceeds $90 and her benefits are reduced by 58c for each dollar of earnings; her earnings increase, therefore, only by $10 * (1-.58) = 4.20 per additional hour; 4) after 108.5 hours of work, she is off the welfare and the slope of the remainder of her budget constraint is 10 again.

Any preferences (utility
function) resulting in indifference curve that meet the budget constraint at
any point to the left of A will make Elizabeth choose to work. (A couple of
examples – U1 and U2 are shown in the diagram below).
Note that the welfare policy described in the problem creates a kink in the budget constraint at 9 hours that makes it individually rational to choose not to work more, although more work is higher earnings. Even much higher wage may be insufficient to pull her out of the welfare trap. The diagram below shows what happens to her budget constraint if she can work for $20 per hour (dashed lines). As indifference curve U2” demonstrates she would choose to work less, earning same $90 as before – and working twice less hours.

Ch. 7. #4
The problem with social programs other than cash transfers is that they may yield less value to the recipient than it costs to the benefactor (government). The question of whether someone is made $x better off by a policy that costs $x should be answered by comparing the utility level reached by the beneficiary of a particular program with the one that would be reached if he or she given $x in cash. In general, this utility is going to fall short of $x, although the answer depends, of course, on the recipient’s preferences. For valuation of in-kind transfers, see pp. 150-52 of the textbook…
In a similar fashion we can analyze the effect of programs like housing assistance that pays a share of housing costs. Its ultimate effect is to change the relative price of housing for the beneficiary.
In the diagram below, O1-H1 is the original budget constraint (we can assume the quantities are measured in some units that make the relative prices of the two types of goods equal to one). A housing assistance program that covers 50% of rent, whatever the rent is, makes the price of housing for the beneficiary twice lower. Budget line goes steeper now: O1-H2.
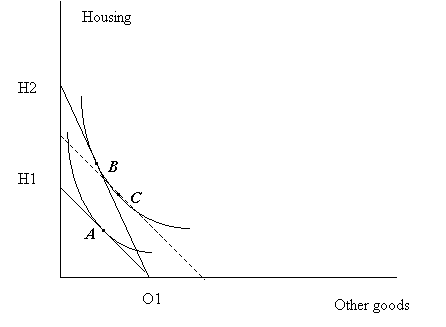
The original optimal choice for the individual with the preferences rendered by the indifference curves in the diagram above is at point A. Once she starts receiving housing assistance, she chooses to have more (better, more expensive) housing and somewhat less other goods (point B). Naturally, her utility increases – moves to the higher indifference curve.
The question is now how much cash should she be given – instead of share-of-cost housing assistance – so that she could reach the same higher indifference curve. We find the answer by shifting the original budget constraint O1-H1 until it is tangent to the higher indifference curve (point C). Position of this imaginary budget constraint – dashed line – relative to O1-H1 tells us about the needed increase in budget (cash transfer).
If we have specific numbers we can evaluate the efficiency of the housing assistance program. Let’s the beneficiary’s monthly budget is $1000, housing expenditure before assistance is $500 (at point A). With the assistance, the beneficiary rents a unit that costs $1200 per mo, actual housing expenditure is $600, and the government (i.e. tax payers) pays $600. At the same time, we might find out that the cash of transfer of only $500 would shift her budget constraint to the position of the dashed line in the diagram. Her utility would increase by the same proportion (the same indifference curve reached) but a lower cost for the society: $600-$500 = $100 net gain. Note also that at the point of optimal choice with cash transfer (point C), her demand for housing increases to a lesser extent and more other goods are bought – more balanced consumption comparing to share-of-cost housing assistance.