ABSTRACT

DISCUSSION

Graphics methods.

Pentilings.

Crystalline Phase Alloys.

Kepler's Pentagon Tiling.

Pentangulation.

Fibonacci Pentilings.

Reordering Pentilings.

Diffraction Patterns and Patterson Functions.

Quasicrystal Crystallography.

Decagonal Quasicrystal Structures.

Conclusion.

FIGURES

FIG. 1. Dürer's pentilings.

FIG. 2. Projected electron density map of FeAl₃ phase alloy and superimposed P₀ = 2 pentile lattice.

FIG. 3. Kepler's tiling with pentagons and decagons and a P = 34 pentiling generated from Kepler's matrix.

FIG. 4. Iterative pentangulation of the P₀ = 2 pentiling.

FIG. 5. Periodic pentilings with more than two pentagons per unit cell.

FIG. 6. Superposition of Kepler's and Penrose's pentagon tilings.

FIG. 7. Diffraction patterns of regular pentilings.

FIG. 8. Patterson maps of regular pentilings.

FIG. 9. Embellished P₈ = 89 Patterson map from Fig. 8.

FIG. 10. Indexing of the P₈ = 89 diffraction pattern.

Table 1. Fibonacci Pentilings.

REFERENCES

This paper was presented at a colloquium entitled "Symmetries Throughout the Sciences," organized by Ernest Hendley, held May 11 and 12, 1996, at the National Academy of Sciences in Irvine, CA.

Five-fold symmetry in crystalline quasicrystal lattices

DONALD L. D. CASPAR AND ERIC FONTANO

Institute of Molecular Biophysics, Florida State University, Tallahassee FL 32306-4380

ABSTRACT     To demonstrate that crystallographic methods can be applied to index and interpret diffraction patterns from well-ordered quasicrystals that display non-crystallographic five-fold symmetry, we have characterized the properties of a series of periodic two-dimensional lattices built from pentagons, called Fibonacci pentilings, which resemble aperiodic Penrose tilings. The computed diffraction patterns from periodic pentilings with moderate size unit cells show decagonal symmetry and are virtually indistinguishable from that of the infinite aperiodic pentiling. We identify the vertices and centers of the pentagons forming the pentiling with the positions of transition metal atoms projected on the plane perpendicular to the decagonal axis of quasicrystals whose structure is related to crystalline phase alloys. The characteristic length scale of the pentiling lattices, evident from the Patterson (autocorrelation) function, is ~ ² times the pentagon edge length, where is the golden ratio. Within this distance, there are a finite number of local atomic motifs whose structure can be crystallographically refined against the experimentally measured diffraction data.

     Quasicrystallography has developed into an elaborate discipline since 1984 when Shechtman et al. (4) first reported crystal-like diffraction patterns with forbidden icosahedral symmetry from aluminum-manganese alloys, and Levine and Steinhardt (5) coined the name quasicrystals for the class of quasiperiodic structures. Exposition of the results of many experimental studies on these novel alloys, and of the efforts of physicists to model their properties are presented in the book Quasicrystals: a primer by Janot (6); and the mathematical concepts involved in the construction of aperiodic lattices are described in Quasicrystals and geometry, by Senechal (2).

     In their endeavors, quasicrystallographers have utilized a variety of mathematically sophisticated but physically unrealistic models to analyze aperiodic lattices with icosahedral or decagonal symmetry. Quasicrystal structures have been represented as projections into two- or three-dimensional space from periodic models in five- or six-dimensional space. For example, such procedures have been applied by Steurer and his colleagues to calculate five-dimensional Fourier maps from three-dimensional X-ray diffraction patterns of decagonal phase aluminum-transition metal alloy quasicrystals (7,8,9). Projections from these physically abstract five-dimensional constructs produce real space maps which show correlations with the crystallographically-determined atomic arrangements in related periodically ordered alloys (10,11,12). The success of this five-dimensional quasicrystallographic analysis suggests that, because the diffraction data is only observable in three-dimensional reciprocal space, more conventional crystallographic analysis might be applied to refine real space models of the atomic arrangements in these quasicrystals.

     Quasicrystals are, by definition, aperiodic lattices. The diffraction pattern from one portion of such a lattice is indistinguishable from that of another portion. A representative portion of a quasicrystal lattice can be chosen as a large unit cell of a perfectly periodic lattice that would yield the same diffraction pattern as the aperiodic lattice. A great variety of such periodic lattices can be constructed by selecting different portions of the aperiodic lattice as the unit cell. The fact that such lattices exist suggests that one member of this class might be transformed into any other member by localized displacive rearrangements of the constituent atoms.

     Our surmise is that quasicrystals with icosahedral or decagonal symmetry may be modeled by periodic packing arrangements of icosahedra or pentagons in moderate-size unit cells that can be locally rearranged, conserving key bonding relations, to generate aperiodic lattices. In this paper, we focus consideration on regular arrangements of pentagons in the plane, applying the same sort of packing rules as used by Dürer (13), Kepler (1) and Penrose (3) in their explorations of pentagonal tilings. The designs of these regular pentagonal tilings are related to the arrangement of transition metal atoms projected on the plane perpendicular to the axes of local five-fold symmetry in the alloys with aluminum of the crystallographically regular phase (10,11,12) and the decagonal quasicrystals (7,8).

     Graphics methods. To visualize the regular arrangements of pentagons (pentilings), their relation to crystal structures, quasicrystal diffraction patterns and Patterson functions, special purpose graphics routines were developed. All images were created and rendered using unique code in the PostScript language (14). Pentilings were created using recursive routines, and coordinates needed for Fourier analyses were generated from the PostScript code using the Aladdin Ghostscript interpreter. Once in PDB format, the coordinates were used with the CCP4 package (15) to calculate electron density maps, structure factors and Patterson maps. The maps were converted to grayscale images and then embedded in PostScript documents. The construction of twinned lattice images and montages utilized the PostScript clipping and superposition capabilities.

     Pentilings. We define a pentiling as an arrangement of regular pentagons in the plane in which each pentagon makes edge-to-edge contact with two, three, four or five neighbors, thereby sharing vertices in such a way that no gaps large enough to contain another pentagon are left in the array. A periodic pentiling is a regular lattice with P pentagons in the unit cell. P is called the pentile number.

     The simplest and most compact periodic pentiling is the first tile pattern formed by pentagons that was described by Dürer (13) in A manual of measurements of lines, areas, and solids by means of compass and ruler, which he published in 1525. This tile pattern (which was illustrated by Dürer in his Fig. 24) is shown in Fig. 1a. The pentile number for this lattice is P₀ = 2, the zero subscript indicating that this is the fundamental member of its class.

     The repeating motif of the P₀ = 2 pentiling (Fig. 1a) consists of the two regular pentagons of edge length E and the 36° lozenge gap, also with edge length E. The crystallographically defined unit cell is the parallelogram with short axis a₀ = E, long axis b₀ = ²E and included angle = 108°, where is the golden mean ( = ² - 1 = ^-1 + 1 = ½(5+1) = 2 cos 36° = (2 sin l8°)^-1 = 1.618034...). The unit cell can also be represented by the 36° lozenge of edge length ²E. Because the ratio of the edge length of the unit cell lozenge to that of the gap is ², the fraction of the unit cell area occupied by pentagons, defined as the packing density, is ₀ = (1 - ^-4) = 0.854102. Each pentagon is joined to three neighbors, thus the coordination number is C₀ = 3.

     Dürer (13) demonstrated that the P₀ = 2 pentiling can be perfectly pentagonally twinned (Fig. 1b). He wrote: "you can combine pentagons in the following manner: First draw a pentagon and place pentagons of the same size on each side. Then place ... pentagons on their sides ... . This will result in the formation of five narrow lozenges between them. Then add pentagons in the angles which will have formed, so that these will touch the narrow lozenges with their corners. You can continue in this manner as long as you desire." The twinning interrupts the regular translational symmetry and produces one five-coordinated pentagon, but does not alter any of the other local contact relations.

     Dürer's P₀ = 2 pentiling appears in various guises in the structure of matter. For example, this pattern was found by Kiselev and Klug (16) in the cylindrical surface lattices formed by pentamers of papovavirus coat proteins that they called pentamer tubes. In the 72 pentamer icosahedral virus capsids of this oncogenic family (17), the 12 pentavalent pentamers make edge-to-edge contacts with their neighbors, as in the pentagonal dodecahedron; but the 60 hexavalent pentamers utilize, in addition to an edge-to-edge contact, one overlapped corner and two point-to-point contacts. In various polymorphic aggregates of polyoma virus pentamers (18), different combinations of these adaptable contacts occur. Thus, the polymorphic packing of these virus pentamers is too complex to be analyzed using the simple pentiling notions that are appropriate for decagonal quasicrystals.

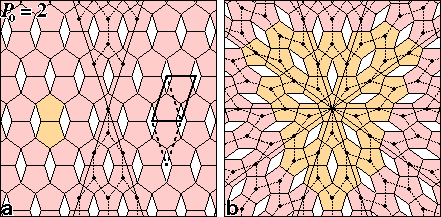
FIG. 1: Dürer's pentilings. (a) The repeating unit of the P₀ = 2 pentiling consists of two pentagons (orange) and one lozenge gap arranged with c2mm plane group symmetry. The primitive unit cell is marked by solid lines or dashed lines in the alternate lozenge shape. The pair of 36° wedge regions, comprising a fifth of the pentile lattice, was used to construct the pentagonally twinned lattice (b) by applying five-fold rotation symmetry about the central pentagon. The twinning of the P₀ = 2 pentiling does not alter the local coordination pattern marked by dotted lines. The ten boundary twinning lines mark rows of pentagons that are shared by neighboring P₀ = 2 lattice domains oriented at 36° to each other. The orange pentagons simulate Dürer's twinning pattern (13).

     Crystalline Phase Alloys. The arrangement of transition metal atoms in the crystalline, phase alloys with aluminum can be modeled in two dimensional projection by Dürer's P₀ = 2 pentiling. Fig. 2 illustrates the projected atomic structure of the FeAl₃ intermetallic compound determined by Black (10). All the crystals he examined were twinned. One of the twinning arrangements he inferred from his atomic model (11) is illustrated at the right side of Fig. 2. The regular pentiling does not perfectly fit the map of Black's projected unit cell because the ratio of the long to short axes from his measurements is 1.6108 ± .0005 rather than the expected golden ratio 1.6180, and his included angle is 17 short of the expected 108°. These discrepancies are so small that they are hardly discernible in the frame of this figure which contains about 18 of the 7.745 × 12.476 Å two-dimensional unit cells. (In three dimensions, the lattice is c face centered, which doubles the 7.745 Å a axis for the crystallographic unit cell.)

     The dark electron density peaks in Fig. 2 correspond to projections of pairs of iron atoms along the direction of the 8.083 Å monoclinic axis. It is evident that the iron atoms, in projection, are located very nearly at the vertices and centers of the regular pentagons of the P₀ = 2 pentiling. The arrangement of the lighter aluminum atoms surrounding the iron atoms, as seen in the projected electron density map, is more complicated, but these details will not concern us in relating possible arrangement of the transition metal atoms to various pentilings.

     Cobalt and aluminum form an phase alloy (12) with structure and twinning very similar to that of FeAl₃, with which it forms solid solutions. The projected unit cell dimensions of 7.592 × 12.340 Å with included angle 107°54 are close to those of the iron alloy. For the cobalt alloy, the axial ratio is 0.46% greater than , whereas with iron it is 0.44% smaller. There are some small but non-trivial differences in the number and arrangement of the aluminum atoms in these two crystals, which suggest some adaptability in the aluminum coordination that maintains the pentagonal arrangement of the transition metal atoms in different lattices and different environments. For example, along the twinning line marked in Fig. 2, the iron atom arrangement is common to the differently oriented lattice domains, but small rearrangements of some of the aluminum atoms must be involved in this meshing.

     In the Fe and Co phase alloys, the transition metal atoms are arranged at the corners of pentagons of mean edge lengths 4.78 and 4.70 Å in flat planes separated by 4.04 and 4.06 Å respectively in the direction of the monoclinic axes of double these separations. The transition metal atoms on the pentagon axes are located about 0.25 Å above or below the midplane of the pair of pentagons and are spaced alternately closer together and further apart along the axes of the pentagonal prisms. In each column, the shorter axial separation is opposite the longer separation in the three neighboring prisms. Some of the details of the three-dimensional arrangement of the transition metal atoms in the pentagonal prisms of the phase crystals will be relevant for considering possible quasicrystalline arrangements. But what we are concerned with at this point is the question: Are there periodic pentilings that can conserve the local pentagonal arrangement of the two-dimensionally projected phase lattice which would allow discrete disordering to form a quasiperiodic lattice? It is evident that localized displacive rearrangements can not be made in the regular P₀ = 2 pentiling.

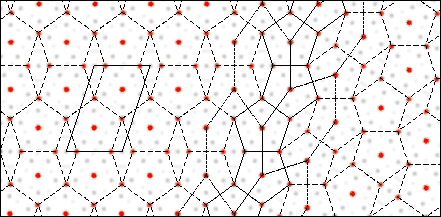
FIG. 2: Projected electron density map of FeAl₃ phase alloy and superimposed P₀ = 2 pentile lattice. The density map was constructed from the atomic coordinates (10), applying a temperature factor of 5 Ų to all atoms and projecting the density on the plane perpendicular to the monoclinic b axis. The twinning was modeled by rotating a portion of the map by 36° and rejoining as illustrated in Fig. 1b. The regular P₀ = 2 pentiling, marked by the dashed lines, closely fits the map with the iron atoms located at the vertices and centers of the pentagons of mean edge length E = 4.78 Å. The common set of pentagons at the twinning boundary is marked by solid lines, with portions of the pattern connecting pentagon centers on either side of the boundary indicated by fine dashed lines.

     Kepler's Pentagon Tiling. Consideration of Kepler's orderly arrangements of pentagons (1) led to insight into ways in which periodic pentilings may be aperiodically disordered. Kepler's tiling with pentagons and decagons from Fig. Aa of his Harmonices Mundi Book II is shown in a computer graphics facsimile in Fig. 3a. Senechal (2) considered this a nonrepeating pattern and concluded that Penrose's first pentagonal tiling family (3) (cf. Fig. 6) is essentially a completion of Kepler's Fig. Aa. In his description of the procedure he used to combine pentagons and decagons in this figure, Kepler commented: "If you really wish to continue the pattern, certain irregularities must be admitted, two decagons must be combined ... . So as it progresses this five-cornered pattern continually introduces something new." However, examination of his pattern shows that a basic repeating unit can be outlined by connecting the star centers to form the elongated hexagons marked in Fig. 3a. These hexagon units have exactly the same shape and packing arrangement as those formed by connecting the pentagon centers in Fig. 1b of Dürer's perfect pentagonal twinning of the P₀ = 2 pentiling. Adding pentagons to extend the regular pattern of Kepler's tiling, we can say with Dürer: "You can continue in this manner as long as you desire."

     Kepler's repeating unit can be assembled into a lattice with perfectly regular translational symmetry, as shown in Fig. 3b. Each decagonal cavity can be fitted with three pentagons and each pair of fused pentagons with six. This completed tiling has pentile number P = 34. The three pentagons in each decagon can be placed in 10 different orientations conserving the number of possible edge-to-edge contacts. There are 52 ways in which the six pentagons can be fitted into the fused decagon pair conserving edge-to-edge contacts. (There are 12 more ways that these pentagons can be fitted without overlap which sacrifice an edge-to-edge contact, but these are excluded by our local packing rule for optimizing contacts.) Therefore, there are 5,200 ways in which 12 pentagons can be added to Kepler's 22 pentagon matrix to conserve the number of contacts and packing density (There are, however, only 1,314 combinations with non-identical autocorrelation functions, counting up-down and enantiomorphic pairs only once.) The pentagons forming Kepler's matrix can also be conservatively reoriented. For example, the five pentagons bordering each pentagram can be flipped in 15 different combinations. Thus, there are an extremely large number of isomers of the P = 34 pentiling, and a larger number of ways in which any of these regular lattices can be discretely disordered, conserving the number of contacts and packing density.

     It is evident that the transition metal atoms in the phase alloys could be arrayed in pentagonal columns corresponding to the pentagons of any of the isomeric or discretely disordered P = 34 pentilings, conserving very similar local packing arrangements. Our surmise is that all the isomers and discretely disordered versions of the P = 34 pentiling just described will have very similar autocorrelation functions, and therefore similar diffraction patterns. We will compare diffraction patterns and Patterson (autocorrelation) functions of different pentilings after more systematic analysis of their designs and packing properties.

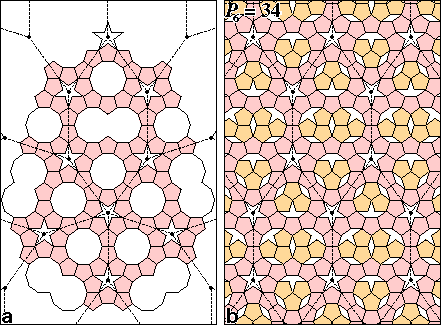
FIG. 3: (a) Kepler's tiling with pentagons and decagons (1) and (b) a P = 34 pentiling generated from Kepler's matrix. The pattern formed by connecting the pentagrams in (a) can be continued indefinitely, as in Fig. 1b, to construct a perfect pentagonal twin of the elongated hexagonal units comprised of 22 pentagons, two decagons, two fused decagons and two pentagrams. By arranging Kepler's matrix unit with translational symmetry and filling the decagonal spaces with twelve pentagons, a regular P = 34 pentiling is formed in (b). Flipping some pentagons at random will produce an aperiodic tiling.

      Pentangulation. How can the possible periodic pentilings with P > 2 be systematically enumerated? An obvious strategy is that used by Penrose (3) to generate aperiodic tilings with pentagons: starting with a pentagonal array of pentagons, each pentagon was subdivided into six smaller pentagons and the gaps in the array between the larger pentagons were filled with the smaller ones; and this process was iterated. Geometers call this process substitution tiling (2). In our application of this substitution tiling strategy to enumerate periodic pentilings, we call the process pentangulation by analogy with the triangulation process used to enumerate possible icosahedral surface lattice designs in the quasiequivalence theory of icosahedral virus construction (19).

     As illustrated in Fig. 4, pentangulation of P₀ = 2 generates a pentiling with P₄ = 13 (the significance of the subscript will be described shortly); pentangulation of P₄ = 13 generates P₈ = 89; and pentangulation of P₈ = 89 generates P₁₂ = 610. The series 2, 13, 89, 610, 4181, ... are the fourth order Fibonacci numbers starting with 2. As a reminder, the Fibonacci numbers are defined: F_n+1 = F_n + F_n-1, with F₀ = 0, F₁ = 1 and F_-n = (-1)^n-1F_n; and starting from F₀, the series begins: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ... . Thus, the series of pentangulations starting with P₀ = 2 have pentile numbers: F₃, F₃₊₄, F₃₊₈, F₃₊₁₂, ... . The pth pentangulation of P₀ (designated by the superscript p) is: P₀^p = P_4p = F_3+4p. In general, P_i = 7 P_i - P_i^-, where P^- is the inverse pentangulation.

     At each pentangulation, the ratio of the edge length of the smaller to the larger pentagons is ^-2; or if we consider the pentagon size to remain constant on pentangulation, the edge length of the unit cell will increase by ² and its area by ⁴. Thus, the fraction of the area occupied by pentagons after the pth pentangulation is _4p = P_4p/^4pA₀ where is the unit pentagon area and A₀ is the area of the P₀ = 2 unit cell. Since /A₀ = ½(1 - ⁴), _4p = (P_4p/2^4p)(1 - ^-4). For P₄ = 13, ₄ = 0.8099767; for P₈ = 89, ₈ = 0.8090374; and for P₁₂ = 610, ₁₂ = 0.8090174. It is evident that the pentagon packing density on successive pentangulations starting with P₀ = 2 converges to = /2 = 0.8090170.

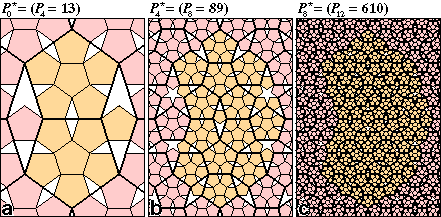
FIG. 4: Iterative pentangulation of the P₀ = 2 pentiling. In the basic pentangulation process (a), six small pentagons are fit into each of the two larger pentagons of the P₀ = 2 pentiling and a single small pentagon is fit into the lozenge gap to generate the P₄ = 13 pentiling. The repeating unit of P₄ = 13 comprises 13 pentagon centers, 29 pentagon vertices, one pentagram, one trigram and three lozenge gaps. Because five small pentagons fit in the pentagram gap and three fit in the trigram gap, the next stage of pentangulation (b) generates P₈ = 6 × 13 + 5 × 1 + 3 × 1 + 1 × 3 = 89 pentagons. Continuing this process (c), pentangulation of P₈ = 89 generates P₁₂ = 610.

     Fibonacci Pentilings. The fact that the pentangulations of P₀ = 2 generate a fourth order sequence of Fibonacci pentile numbers, and the P = 34 pentiling generated from Kepler's net represents another Fibonacci pentile number, suggests that the sequence of pentilings with P_n = F_n+3 may be particularly relevant for characterizing the geometry of decagonal quasicrystals. Nevertheless, it is possible to produce periodic pentilings with any number of pentagons 2 in the unit cell.

     Fig. 5 illustrates regular pentilings for P = 3, 4, 5 and 8. Two versions of P = 4 are shown, to demonstrate that this is not a very interesting pentile number. The P = 4a pentiling has exactly the same pentagon packing density as P₀ = 2, and can be generated from it by multiple twinning along the oblique rows using Dürer's scheme shown in Fig. 1b. The alternate P = 4b arrangement has a considerably lower pentagon packing density than any of the other illustrated pentilings. The packing density in any periodic pentiling can be calculated by dividing the area of the pentagons in the unit cell by the total pentagon and gap areas. There are three different size gaps in a regular pentiling that are allowed by our local packing rules: a lozenge L; trigram (Penrose's "paper boat") T; and pentagram (star) or allopentagram (as in the P = 4b pentiling) S. The relative areas of these gaps, taking the pentagon area = 1, are L = 2(3 + 1)^-1, T = ( + 3)(3 + 1)^-1 and S = 2^-1. Thus, (P = 4b) = 2^-2 = 0.763932. Successive pentangulation of P = 4b gives packing densities that converge to /2. (The first pentangulation generates P = 29 with = 0.808057 and the second generates P = 199 with = 0.808997.)

     For the Fibonacci pentilings we enumerate in Table 1, the pentagon packing density converges more closely with increasing pentile number to /2 than for any other pentiling not in this class. The closer the packing density is to /2, the more exactly the periodic pentiling represents the ideal of an infinite aperiodic array. All possible Fibonacci pentilings can be derived by pentangulation starting from the P₀ = 2 already described, and the P₁ = 3, P₂ = 5 and P₃ = 8 pentilings illustrated in Fig. 5. Furthermore, these pentilings can all be twinned with themselves, or twinned with each other in various combinations, as illustrated in Fig. 5 for a particular combination of P₂ = 5 with P₃ = 8.

     It is evident from Fig. 1 and Fig. 5 and the rule for pentangulation that the unit cells for Fibonacci pentile numbers of even index (P_2m = 2, 5, 13, 34, ...) are 108° parallelograms with edge lengths a = ^m+1E and b = ^m+2E, where E is the pentagon edge length; for the odd index Fibonacci pentile numbers (P_2m+1 = 3, 8, 21, 55, ...) the unit cells are 108° rhombs with edge length a = b = ^m+2E. Thus the area of any of these unit cells with pentile number P_n = F_n+3 is A_n = ⁿA₀, and the pentagon packing density _n = P_n/A_n = ½P_n^-n(1 - ^-4). From the definition of P_n and the relations for the powers of : ⁿ = F_n + F_n-1 and ^-n = (-1)^n-1(F_n - F_n+1), it can be demonstrated that _n = ½[1 + (-1)^{n-(2n + 6)}]. The fractional pentagon density difference (_n - )/ starts at +0.0557281 for P₀ and oscillates between negative and positive values of rapidly diminishing magnitude for successive odd and even index pentile numbers, as listed in Table 1.

     Other parameters listed in Table 1 that are important for characterizing the Fibonacci pentile packings are the mean coordination C_n which defines the average number of edge-to-edge contacts per pentagon; and V_n, the number of pentagon vertices contained within the unit cell. The sum P_n + V_n = 2P_n+1 corresponds to the total number of sites per unit cell (in projection) that could be occupied by transition metal atoms (M) with the geometry of the phase illustrated in Fig. 2. The product _n(P_n + V_n)/P_{n n}(M) is a measure of the density of M atom sites as a function of the order of the pentile number. From the numbers in Table 1, it can be seen that although the density of pentagon centers in the P₀ = 2 pentiling (corresponding to the geometry of the crystalline phase alloys) is 5.57% greater than that of the limiting aperiodic pentiling, the density of total M sites (pentagon vertices + centers) is 2.13% smaller for the P₀ = 2 pentiling than for the aperiodic limit. Thus, less ordered packing arrangements of the pentagonal columns of transition metal atoms can lead to slightly denser M atom packing while maintaining the same nearest neighbor separations. Such a density increase would be accommodated by a reduction in aluminum content.

     It is evident from Table 1 that it is not necessary to go to a very large pentile number to reach a pentagon packing density that would be experimentally indistinguishable from the infinite limit of /2. Furthermore, the occurrence of only a small number of local motifs in these large period pentilings suggests that ordered lattices with moderate size periods may provide adequate models for less ordered states.

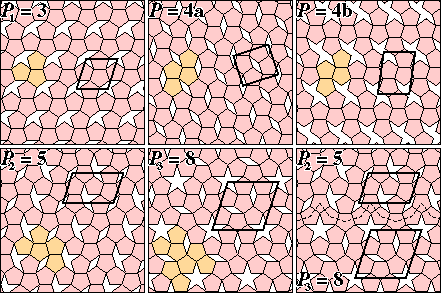
FIG. 5: Periodic pentilings with more than two pentagons per unit cell. Pentagons in a repeating unit are orange and unit cells are marked by solid lines. The regular Fibonacci pentilings P₀ = 2, P₁ = 3, P₂ = 5 and P₃ = 8 are the first four members of the series listed in Table 1 whose pentagon packing densities are approximately /2. As explained in the text, the two versions of P = 4 illustrated have packing densities that differ significantly from that of the closest Fibonacci pentilings (P₁ = 3 and P₂ = 5). Different pentiling lattices can be twinned with themselves or each other in various combinations. P = 4a corresponds to periodic twinning of P₀ = 2. The illustrated twinning of P₂ = 5 and P₃ = 8, with the common boundary marked, exemplifies one of the many ways in which periodic pentilings can be combined to generate less regular pentilings.

Table 1. Fibonacci Pentilings

Pentile Number P_n = F_n+3 number of pentagons in unit cell. (F_n+3 is sequence of Fibonacci numbers, starting with 2.) Pentagon vertex number V_n = P_n + 2P_n-1 number of pentagon vertices in unit cell. Mean number of M atom sites per pentagon (P_n + V_n)/P_n = 2P_n+1/P_n; asymptotic value = 2 = 3.236068. Mean pentagon coordination C_n = (P_n+1 + P_n-4)/P_n; asymptotic value = ² + ^-4 = 2.763932. Pentagon packing density _n = ½P_n^-n(1 - ^-4) = ½[1 + (-1)^{n-(2n + 6)}]; asymptotic value = /2 = 0.809017. M atom site density _n(P_n + V_n)/P_{n n}(M) = ²[1 + (-1)^n+1-(2n+8)]; asymptotic value = ² = 2.618034. Values for (_n(M) - (M))/(M) = (-1)^n+1-(2n+8) are not listed because this is equal to (_n+1 - )/ which is listed for the succeeding pentile number.

n	Pn	Vn	(Pn + Vn)/Pn	Cn	(n - )/
0	2	4	3	3	+5.5728 × 10-2
1	3	7	3.33333	2.66666	-2.1286 × 10-2
2	5	11	3.2	2.8	+8.1306 × 10-3
3	8	18	3.25	2.75	-3.1056 × 10-3
4	13	29	3.23077	2.76923	+1.1862 × 10-3
5	21	47	3.23810	2.76171	-4.5310 × 10-4
6	34	76	3.23529	2.76471	+1.7307 × 10-4
7	55	123	3.23636	2.76364	-6.6107 × 10-5
8	89	199	3.23596	2.76405	+2.5251 × 10-5
9	144	322	3.23611	2.76389	-9.6449 × 10-6
10	233	521	3.23605	2.76395	+3.6840 × 10-6
11	377	843	3.23607	2.76393	-1.4072 × 10-6
12	610	1,364	3.23607	2.76393	+5.3749 × 10-7

     Reordering Pentilings. The larger the pentile number, the larger the number of isomers and the greater the possibilities for introducing discrete disorder by flipping pentagons without altering the mean coordination or packing density (cf. Fig. 3b). Such local displacive rearrangements can also transform one ordered pentiling into another with comparable packing density. Fig. 6 illustrates the superposition of Kepler's pentagonally-twinned matrix of pentagons (from Fig. 3a) on the first "aperiodic" tiling presented by Penrose (3). Penrose's tiling can be represented as the second pentangulation of Dürer's (13) pentagonally-twinned P₀ = 2 pentiling to generate the five-fold twin of the P₈ = 89 pentiling. The superposition in Fig. 6 requires 11 pentagon flips within the frame. There are many other ways in which Kepler's tiling, or regularly periodic versions of it, can be superimposed on Penrose's tiling that require different numbers of pentagon flips. These pentagon flips should correspond to energetically equivalent local packing arrangements.

     A pentagon flip in atomic terms corresponds to interchanging a pentagon center and vertex in one orientation for a vertex and center in the other. The displacement in the plane of the pentagon for the two sites is E tan 18°, which, if E = 4.7 Å, involves a lateral movement of 1.5 Å. In the phase alloys (10,12), the axial metal atoms sit ~ 1.7 Å above or below the pentagonal plane. Interchange of axial and vertex positions would involve coupled movements of ~ 2.3 Å. The activation energy for such coordinated movements in columns of atoms might be very high, but could be facilitated by lattice defects designated as phasons in quasicrystallography (6). Even if such flips are rare in the locally well-ordered condensed state, during crystallization columns of atoms would have to choose between pentagon axial and vertex sites. Thus, under conditions favoring a pentagon packing density /2, any of the local atomic arrangements corresponding to moderate-to-larger size periodic pentilings would be equally probable. As we will show, these lattices have virtually indistinguishable diffraction patterns.

FIG. 6: Superposition of Kepler's and Penrose's pentagon tilings. Penrose's tiling (3), marked by the boldly outlined pentagons, is a perfect five-fold twin of the P₈ = 89 pentiling whose unit cells are marked by the portions of the lightly outlined 36° rhombs centered on the starred pentagon. This facsimile of his tiling has been extended 11% to the left of his margin to give the frame a golden aspect ratio. Kepler's pentagonally twinned matrix of shaded pentagons, from Fig. 3a, is centered on a pentagram in a region of Penrose's tiling that has only local five-fold symmetry. The 11 sites within this frame at which pentagon flips are necessary to transform from Penrose's to Kepler's pattern can be recognized by the shaded pentagons that do not match the bold outline. Kepler's matrix cells, outlined with dashes, each contain an isomer of the P₆ = 34 unit, which can be distinguished by the orientation of the twelve pentagons inside the decagonal spaces. Curiously, four of these cells contain the same isomer. The density of the P₆ = 34 pentiling is 0.0148% greater than that of P₈ = 89, amounting to one more pentagon in an area ~ 20× that shown here.

     Diffraction Patterns and Patterson Functions. "Atomic" models based on several of our Fibonacci pentilings were constructed by placing atoms at the centers and vertices of the pentagons. This construction for P₀ = 2 corresponds to omitting the aluminum atoms from the projected map of Black's (10) phase FeAl₃ structure in Fig. 2. A montage of the modeled diffraction patterns and Patterson functions for P₀ = 2, P₄ = 13, P₆ = 34 and P₈ = 89 are shown in Figs. 7 and 8. The arrangement of the pentagons in the P₀ = 2 pentiling has mm symmetry, and arrangements were chosen for the even order pentilings with a line of mirror symmetry perpendicular to the a axis (i.e., along the long axis of the 36° lozenge unit cell). Thus, the Fourier transforms have mm symmetry and the single quadrant displayed for each model in Fig. 7 represents all the diffraction data. The Patterson functions (Fig. 8), were calculated from the squared structure factors illustrated in Fig. 7. All unit cells have the same golden ratio shape because the Fibonacci pentile numbers all have even order indices. The cell dimensions for P₀ = 2 are a = E = 7.60 Å and b = ²E = 12.30 Å; for P₄ = 13, P₆ = 34 and P₈ = 89 these dimensions are scaled up by ², ³ and ⁴ respectively.

     In both reciprocal and Patterson space, the patterns for P₄, P₆ and P₈ show dominant 10-fold symmetry, characteristic of the averaged pentagonal packing of the pentagons in these moderate size unit cells. Small departures from perfect 10-fold symmetry are evident in the P₄ = 13 patterns, but such undecagonal features are more difficult to detect in the P₆ = 34 and P₈ = 89 patterns. For the P₀ = 2 patterns, even though the unit cell axes are at an angle of 108°, there is little indication of 10-fold symmetry. Nevertheless, there are evident correlations in the distribution of the short vectors of the P₀ = 2 Patterson function compared to those of its more pentangulated relations, indicative of the common local atomic packing relations.

     It has been argued (6) that large unit cell models are inappropriate to represent quasicrystal structures because "unit cells in crystal models have to be so large that they would imply a physically implausible range of interaction." We are not proposing that any particular crystal model represents the actual atomic arrangement of a quasicrystal. What we have demonstrated is that a wide range of crystal models with common local pentagonal coordination relations have nearly indistinguishable decagonal Fourier transforms and autocorrelation functions. A priori, any one of our crystal models with a moderate size unit cell is as likely a representation of the actual projected arrangement of the transition metal atoms in a defect-free domain of a decagonal quasicrystal (7,8) as any particular defect-free aperiodic model with pentagon packing density /2. Periodic pentiling models with moderate size unit cells provide a rational foundation for crystallographically refining the actual local atomic arrangements that build up the quasiperiodic decagonal crystal structures.

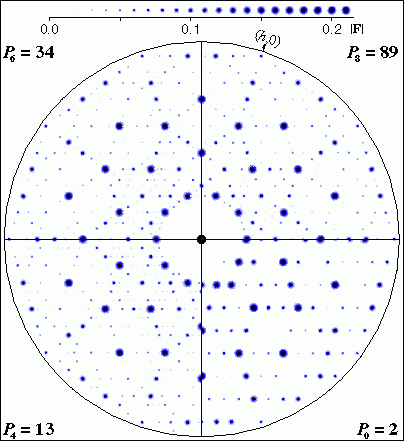
FIG. 7: Diffraction patterns of regular pentilings. Model electron density maps similar to Fig. 2 were calculated by placing identical atoms with temperature factors of 5 Ų at the vertices and centers of pentagons in the P₀ = 2, P₄ = 13, P₆ = 34 and P₈ = 89 pentilings from Figs. 1a, 4a, 3b and 4b respectively. The pentagon edge length E in this construction is 4.7 Å. Fast Fourier transforms of these maps were calculated to 0.9 Å resolution and the amplitudes were scaled by setting F₀₀ to unity. The maximum scaled amplitude in each pattern is |F_max| ~ 0.2. The quadrants, which include all independent Fourier coefficients for each pattern, are aligned with the (0,k) axis horizontal. The patterns from the higher order pentilings have evident ten-fold symmetry. Comparison across the boundary between the P₆ = 34 and P₈ = 89 patterns demonstrates that they are virtually indistinguishable. The structure factors, which are discrete points in reciprocal space, are depicted as Gaussian disks with radii proportional to the amplitudes as indicated in the |F| scale at the top. The intensity range displayed is ~ 100.

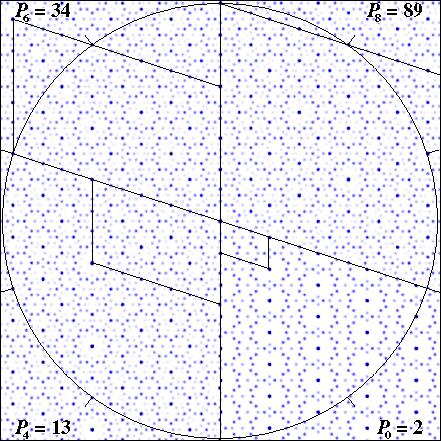
FIG. 8: Patterson maps of regular pentilings. Sectors of the four Patterson maps are aligned with their a axes vertical and their unit cells outlined (the b axis of P₈ = 89 extends beyond the image frame). The circle has radius 52.4 Å = ⁵E, which is equal to the a axis of P₈ = 89 and the b axis of P₆ = 34, and is marked every 36° to emphasize the ten-fold symmetry.

     Quasicrystal Crystallography. For a crystallographer, a crystal is like an orderly forest that is useful for determining the average structure of the trees. The repeating unit may be a clump of trees related by noncrystallographic symmetry or constrained to grow in non-equivalent configurations. These complexities can aid the crystallographer in seeing the trees more clearly. Quasicrystallographers have, however, had difficulty seeing the trees for the forest. The higher dimensional representations of quasicrystalline forests are mathematically elegant, but these abstractions have tended to obscure sight of the trees. It is evident that these atomic trees are locally ordered in clusters that are arranged quasiperiodically. How can the structure of these clumps be most clearly visualized?

     One way to approach the question of how the atoms are arranged in a quasicrystal is to look at the Patterson function that epitomizes all the information about the interatomic vectors contained in the diffraction pattern. Fig. 9 shows an embellished version of the P₈ = 89 Patterson function calculated from the diffraction pattern that is shown indexed in Fig. 10. An obvious feature of the pentiling Patterson, emphasized by the circles drawn about the origin and quasiorigins, is that the characteristic length scale is ~ ² times the pentagon edge length E. The central portion of this Patterson, which is repeated at the quasiequivalent origins, is indistinguishable from that of any pentiling with comparable or larger cell dimensions or from a five-fold average of any of these Pattersons (which would represent the autocorrelation function of the pentiling with infinite size unit cell that is the ultimate quasiperiodic lattice). Thus, the Patterson function solution at the length scale ~ ²E for a suitable crystalline representation of the decagonal diffraction data is a solution for any crystalline or quasicrystalline representation of this data. This data can be analyzed crystallographically.

     Quasicrystallographers have concluded that the diffraction maxima in decagonal patterns, such as in Fig. 10, can not be assigned rational, two-dimensional Miller indices because the Bragg spacings along lattice lines correspond to incommensurate periodicities. There are, however, no incommensurate periodicities in the world of experimental distance measurements. For example, the diffraction pattern from a helix with an irrational screw axis would be indexed by an experimentalist as having u units in t turns. The exact values of u and t depend on the accuracy with which the ratio of the layer-line spacings corresponding to the helix pitch and unit axial translation can be measured. The more precise this measurement, the larger the calculated repeat distance. Indexing a large helix repeat distance does not imply an implausible range of interaction, but does indicate the skill of the fiber diffractionist in making precision measurements. The same considerations can be applied to indexing experimentally recorded quasicrystal diffraction patterns.

     A set of selection rules for indexing the diffraction maxima in the decagonal patterns could be formulated as for helical diffraction, but all that is needed is the choice of pentile model and the rule for indexing the lowest resolution set of strong reflections. Odd and even order pentile numbers correspond to fat and thin golden ratio rhombic unit cells as already noted, and either will represent the decagonal quasicrystal symmetry. For the even order (P_2m) Fibonacci pentile diffraction patterns illustrated in Fig. 7, with unit cell dimensions a = ^m+1E and b = a, the index of the first strong (h,0) reflection along the a* axis is h = P_m (= F_m+3); for the first strong (0,k) reflection along the b* axis, k = P_m+1 (= F_m+4); and for the first (h,k) reflection at ~ 36° between the (h,0) and (0,k), h = P_m-1, k = P_m. These three reflections have very nearly the same Bragg spacing. For the P₈ = 89 diffraction pattern in Fig. 10, for which m = 4, the ratio of the spacings d*_0,21 : d*_8,13 : d*_13,0 is 1 : 0.99949 : 1.00164. For higher resolution decagonally related reflections or for higher order pentiling lattices, these ratios approach much closer to 1 (e.g., d*_34,0/d*_0,55 = 1.00024 and d*_0,89/d*_55,0 = 1.00009). An experimental diffraction pattern can be represented as the five-fold average of a pentile model pattern that best fits the measured width of the Bragg reflections.

     A curious feature of quasicrystal diffraction patterns, associated with what is called phason disorder, is a sharpening of the diffraction peaks with increasing angle (20). Pronounced broadening of low-resolution peaks in decagonal patterns can be accounted for by pentagonal averaging of diffraction from lattice domains with relatively small pentile numbers. For a multiply twinned mosaic of such domains (cf. Fig. 5), whose densities vary above or below the asymptotic value for higher order pentilings (Table 1), the effect on the diffraction pattern would be to enhance small angle diffuse scatter and average decagonally related Bragg peaks with slightly different spacing. This peak broadening would progressively diminish for higher resolution reflections.

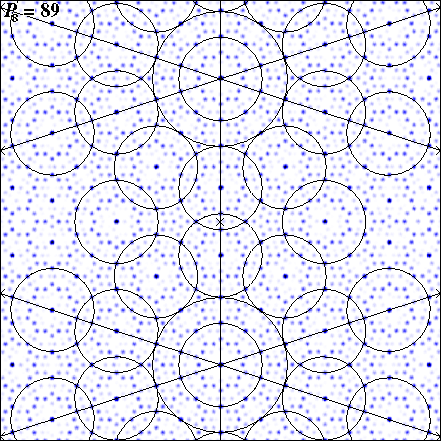
FIG. 9: Embellished P₈ = 89 Patterson map from Fig. 8. Unit cell axes are marked and the a axis is vertical. The map has mirror symmetry parallel and perpendicular to the a axis at the origin and at a/2 marked with a cross. The centers of symmetry at the left and right margins are also marked. Circles of radius E and ²E are drawn about the crystallographic origins. Circles of radius E are drawn about the quasiequivalent origins related by the local noncrystallographic ten-fold axes and the crystallographic centers of symmetry. Circles of radius ²E can also be drawn around the quasiequivalent origins which fit like that about the crystallographic origin.

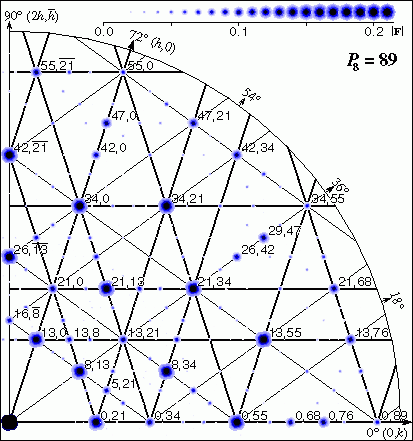
FIG. 10: Indexing of the P₈ = 89 diffraction pattern. The quadrant in Fig. 7 is enlarged and the most intense spots are labeled with their h,k indices. The thick lines, which are parallel to the crystal axes and are spaced at intervals of consecutive Fibonacci numbers, pass through rows of lattice points including the most intense spots. The thin lines, at angles of ±36° to the (0,k) direction, are noncrystallographic but nearly pass through centers of the intense spots related by the noncrystallographic ten-fold symmetry.

     Decagonal Quasicrystal Structures. The two-dimensional pentile lattices appear to provide reasonable trial models for the projected arrangement of the transition metal atoms in the plane perpendicular to the five-fold axes of decagonal quasicrystals such as Al₆₅Cu₂₀Co₁₅ (7) and Al₇₀Ni₁₅Co₁₅ (8). The Bragg spacings for the first equatorial decagonal set of strong reflections - which have been given five-dimensional indices (10000) - are 3.765 and 3.794 Å respectively for these two quasicrystals. The indexing of a pentile lattice diffraction pattern (Fig. 10) indicates that the mean spacing of this set of strong reflections is the limiting value of (P_m)^-1m+1E cos 18°. The asymptotic value of (P_m)^-1m+1 = ^-1 + ^-3 = 1 - ^-4 = 0.854102. Thus, the mean pentagon edge lengths corresponding to the Bragg spacings of 3.765 and 3.794 Å are E = 4.635 and 4.671 Å respectively. These values are in good accord with the density maps projected from the calculated five-dimensional Fouriers (7,8) and the mean edge length of 4.70 Å for the phase Al₁₃Co₄ alloy (12).

     There are many fascinating aspects to the decagonal quasicrystal diffraction patterns obtained by Steurer and his colleagues (7,8). The satellite reflections around the strong Bragg maxima are suggestive of ghost spectra (21) due to microdomain structure or directional quasiperiodic density fluctuations on a long distance scale. The pronounced small angle diffuse scatter is characteristic of uncorrelated density fluctuations on a long-to-moderate distance scale. The strongly modulated diffuse diffraction on the odd order 8.08 Å layer planes perpendicular to the pentagonal prism axes is related to absence of long-range lateral correlations in the up-down displacements of the axial metal atoms that are regularly staggered between adjacent columns in the phase alloys (10,12). Analysis of this diffuse scatter, applying methods developed in protein crystallography (22), could provide a measure of the decay distance for the lateral correlations in the axially staggered displacements and the magnitude of the mean square fluctuations in the lateral positions of the variable atoms.

     From the density maps derived by five-dimensional Fourier analyses of the decagonal quasicrystals (7,8,9) it should be possible to construct real space models which could be refined against the diffraction data using conventional crystallographic least squares methods. The characteristic distance scale evident from the Patterson function (Fig. 9) indicates that the distinctive structural motifs need only be modeled to distances ~ ²E 12 Å, which corresponds, for example, to the vertex-to-vertex span of a pentagram or the center-to-center separation of a pair of pentagons attached to the non-adjacent sides of a central pentagon. Within this distance, there are a finite number of motifs, all or most of which will be represented in any reasonable size periodic pentile lattice. Individual pentagons can be five-, four-, three-, or two-coordinated. The metal atoms at the vertices of a five-coordinated pentagon would be expected to be equivalently related; but in all other pentagon environments, these atoms will be quasiequivalently related, as in the crystalline phase structures (10,11,12), which means that the five edge-length distances need not be exactly equal.

     Experimental diffraction data for the vectors between the transition metal atoms can be obtained by multiwavelength anomalous dispersion measurements. This data would also identify possible correlations in the positions of the two types of transition metals in the stable decagonal quasicrystals. Having established the number of independent variables for these metal atom-metal atom vectors, these vector distances could be refined within the framework of any reasonable size three-dimensional periodic pentile lattice. The number of parameters required to refine all the possible aluminum atom configurations in the distinguishable environments is likely to exceed the 253 independent structure factor terms that have been measured to 0.5 Å resolution for the Al₇₀Ni₁₅Co₁₅ decagonal quasicrystal (8). In this case, stereochemical and energetic restraints could be applied to refine the structure as in macromolecular crystallography (23,24).

     Conclusion. We have demonstrated that in the decagonal quasicrystalline realm, the Emperor need not wear five-dimensional quasiclothes, and we surmise that similar six-dimensional garments will prove to be unnecessary in the icosahedral quasicrystalline domain.

      We thank Bin Yu for assistance with the crystallographic calculations. This work has been supported by a U. S. public health service research grant from the National Institutes of Health's National Cancer Institute, grant number CA47439-08.

1. Kepler, J. (1619) Harmonices Mundi (Facsimile Edition: Forni Editore, Bologna (1969); Book II: On the congruence of harmonic figures. English translation by J. V. Field in Vistas in Astronomy 23, 109-141 (1979)).
2. Senechal, M. (1995) Quasicrystals and Geometry (Cambridge Univ. Press, Cambridge, U.K.).
3. Penrose, R. (1979) Math. Intelligencer 2, 32-37.
4. Shechtman, D., Blech, I., Gratias, D. & Cahn, J. W. (1984) Phys. Rev. Lett. 53, 1951-1953.
5. Levine, D. & Steinhardt, P. J. (1984) Phys. Rev. Lett. 53, 2477-2480.
6. Janot, C. (1992) Quasicrystals: a primer (Clarendon Press, Oxford, U.K.).
7. Steurer, W. & Kuo, K. H. (1990) Acta Cryst. B46, 703-712.
8. Steurer, W. Haibach, T., Zang, B. Kek, S. & Lück, R. (1993) Acta Cryst. B49, 661-675.
9. Haibach, T. & Steurer, W. (1996) Acta Cryst. A52, 277-286.
10. Black, P. J. (1955) Acta Cryst. 8, 43-48.
11. Black, P. J. (1955) Acta Cryst. 8, 175-181.
12. Hudd, R. C. & Taylor, W. H. (1962) Acta Cryst. 15, 441-442.
13. Dürer, A. (1525) A manual of measurement of lines, areas and solids by means of compass and ruler (Facsimile Edition translated with commentary by W. L. Strauss (1977), Abaris Books, Inc., New York).
14. Adobe Systems, Inc. (1990) PostScript Language Reference Manual, second edition (Addison-Wesley, Reading, MA).
15. Collaborative Computational Project Number 4 (1994) Acta Cryst. D50, 760-763.
16. Kiselev, N. A. & Klug, A. (1969) J. Mol. Biol. 40, 155-171.
17. Rayment, I., Baker, T. S., Caspar, D. L. D. & Murakami, W. T. (1982) Nature (London) 295, 110-115.
18. Salunke, D. M., Caspar, D. L. D. & Garcea, R. L. (1989) Biophys. J. 56, 887-900.
19. Caspar, D. L. D. & Klug, A. (1962) Cold Spring Harbor Symp. Quant. Biol. 27, 1-24.
20. Stephens, P. W. and Goldman, A. I. (1991) Sci. Amer. April, 44-53.
21. James, R. W. (1954) The Optical Principles of the Diffraction of X-rays (G. Bell and Sons, London).
22. Clarage, J. B., Clarage, M. S., Phillips, W. C., Sweet, R. M. and Caspar, D. L. D. (1992) Proteins 12, 145-157.
23. Hendrickson, W. A. & Konnert, J. H. (1981) Biomolecular Structure: Conformation, Function and Evolution, Vol. I, edited by R. Srinivasan, pp. 43-57 (Pergamon Press, Oxford, U.K.).
24. Brünger, A. T. (1990) X-PLOR Manual, Version 2.1 (Howard Hughes Medical Institute, Yale Univ., New Haven, CT).