Intro Mind Notes, Week 4: Neurological Theories of the Mind
(HMW, Ch. 2, pp. 98-131)

A. Why Study The Nervous System?

B. The Brain

  1. The brain contains at least 10^11 neurons. (10^11 is 100 billion). Each of these consists of a soma (cell body) dendrites (input fibers) and an axon that terminates in synapses (output terminals).
  2. The brain also contains 10^12 glial cells that cover axons with myelin (a fatty insulator), control and absorb neuro-transmitters, dispose of dead cells, and generally keep the neurons functioning properly.
  3. The brain is usually divided into 3 parts: Forebrain , Midbrain and Hindbrain .
  4. The main parts of the forebrain are the cerebral cortex (or cortex for short) and the limbic system .
  5. The cortex consists of approximately six layers of neurons spread over about one square yard, all crumpled up in the shape of a walnut, with two sides joined by the corpus collussum . The top surface is called the grey matter, and is composed of cell bodies (soma). Underneath is white matter which is composed of axons covered with myelin, which is white.
  6. The limbic system lies underneath the cortex and is concerned with emotion and motivation.
  7. One of the largest structures in the Hindbrain is the cerebellum , which fine tunes muscle control for smooth coordination.

C. How Neurons Work

  1. Ion pumps in the cell wall maintain a difference in charge (called a membrane potential) across the cell membrane, so that the inside is negative, and the outside is positive.
  2. But there are channels that can open to let positive charge back into the cell (or let negative charge out) and cancel the negative inside charge near the channel. This is called depolarization of the cell wall.
  3. When channels open at the root of the axon, the reduction of the charge difference (membrane potential) causes neighbor channels to open as well. This causes a cascade of openings (depolarization) down the axon all the way down to its synapses.
  4. At a synapse, the change in charge causes little sacs full of neurotransmitters (called synaptic vesicles ) to open into the cell wall, exposing the cell wall of the neighboring neuron's receptor sites to the neuro-transmitter. Depending on the neurotransmitter and receptor site, the presence of the neurotransmitter may inhibit or sensitize the neighbor neuron to possible future depolarization.
  5. The effects at all the synapses of the neighbor neuron add together. If there is enough over all activity at the base of its axon, the channels there will depolarize and the neighbor cell will fire.

D. Neural Plasticity

  1. During early development, neural structure is often formed by the elimination of excess neurons and synapses.
  2. The development of structure depends on the stimulation the brain receives, and when it occurs. If a sighted child is blindfolded during the critical period for creation of sight structures, the ability to see will have great difficulty developing. The same sort of critical period appears in the case of the recognition of phonemes (language sounds) and the ability to process grammatical structure.
  3. If a child loses cortex normally devoted to such functions before the critical period there is a good chance another region of cortex will take over. So the brain is plastic at an early age.
  4. However after a critical period, lost of the relevant part of the brain means that the ability cannot be restored, or is restored with great difficulty.

E. Brain Regions and Topographic Maps

  1. In a normal brain, there are standard locations in cortex of the basic functions (although there are some variations as well). Here is a crude picture of a left hemisphere:


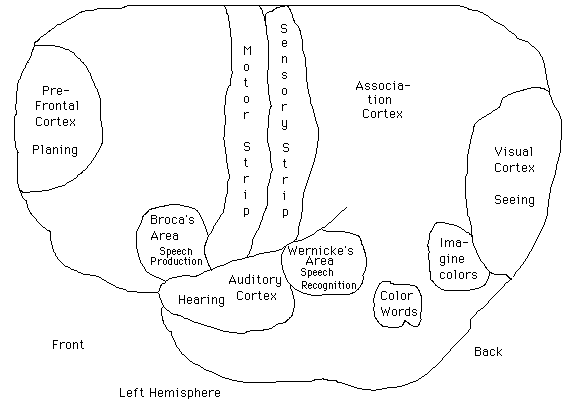
  2. Motor, sensory, auditory and visual cortex are all arranged in topographic maps. This means that regions in cortex correspond to regions of the body, the retina, or the cochlea (the main sensory organ of the ear). For example, parts of sensory cortex respond to stimulation of the palm, and nearby ones to the thumb etc.. In auditory cortex, some neurons are devoted to low pitch, and their neighbors to slightly higher pitch and their neighbors to pitches higher still etc.. An area such as visual cortex may have many different topographic maps devoted to different functions, such as general shape detection, motion, and color. To some extent, the specific regions dedicated to a given sensory region vary depending on much stimulation is received there. So the brain is still somewhat plastic at the micro-level.

F. Neural Representation

  1. Is there a grandmother neuron, a neuron that fires when I see a grandmother? Almost certainly not. Brain representations are distributed across many neurons. So the representation of my grandmother is no doubt the combination of many many neurons coding for lots and lots of features that make up my grandmother experience: color of hair, facial shape, gait, sound of voice, etc..
  2. Neural representation often uses what is called distributed representation . We illustrate this in the case of color vision. You might think that there are neurons that are responsive to particular wavelengths of light, say neurons for 500 nanometers, for 510 nanometers, etc.. But color vision depends on the fact that we have 3 different kinds of cones (sensory neurons) (called S, M, L) that respond somewhat differently to color. These cones have a very large region of wavelength overlap so that for most colors, all 3 kinds of cones are active at least to some degree. The representation of the color red, for example, corresponds to a characteristic amount of activity on the S, M and L cones. (So there really aren't any red green or blue cones as some popularizations would have it .) Green has its own pattern of activity, and so on for the other colors. This means that a color sensation is represented as a triple of numbers indicating the activity of S, M, and L. This kind of distributed coding is surprisingly efficient.
  3. A similar representation is used to code tastes, but here there are 4 not 3 styles of tasters neurons (roughly for salt, sweet, sour, bitter).
  4. Another example if distributed representation concerns control of movement. Say I plan to throw a dart to a target. The direction of a target is distributively coded as a collection of activities on various neurons. How can this information be used by the brain to control the arm to throw the dart? Is it ever averaged together in one place in the brain? Probably not. The brain just sends the raw collection of directions in parallel to motor output to control the direction of the target. The slightly contradictory muscle movements will average out in the arm, and you will get the job done.

G. Radical vs. Implementational Connectionism

  1. The fundamental connectionist idea is to build models of cognition that are guided by the nature of neural processing, but to abstract away from irrelevant neural features. There are three different ideas about how the classical or information processing account relates to connectionist theories.
  2. Implementational connectionists will view their role as explaining how information processing is implemented in the brain. They pretty much accept the classical account, and attempt to explain how the processing described by classicists could be carried out in the brain's neural nets. It is a simple matter to show that neural nets can carry out the basic operations of a Turing Machine, so in principle it can manage any symbolic computation.
  3. Radical connectionists like Rumelhart and McClelland view their theories as competitors to classical ones. The idea is that classicists have an incorrect theory about what cognition is like, and that neural networks (Pinker calls them connectoplasm) can replace the information processing account. Naturally, radical connectionists and classicists have engaged in hot debate. Garson tends towards the radical side of the controversy.
  4. Hybrid connectionists think that connectionism best describes only some of our cognitive abilities, notably those in perception, pattern recognition, and motor control. Classical theories are needed to explain other abilities such as reasoning and language. So hybrid connectionists are radical for some abilities and implementational for others. This is the view that Pinker takes.

H. Neural Networks: The Basics

  1. Units and Weights. Neurons add together the effects of their neighbor neurons (i.e.the neurons that send signals to them). Depending on the nature of the synapse(s) between them, the neighbor neuron's activity may either inhibit or excite the activity of the target neuron. Connectionists model neurons with simple processors called units . The synapses which regulate signals between neurons are modeled by values called weights . Weights can be positive (indicating that activity at the synapse encourages the neighbor neuron to fire) or negative (indicating that activity at the synapse inhibits firing by the neighbor neuron).
  2. The Activation Function. It is assumed that all units calculate the same very simple function called the activation function . The fundamental idea is that the target unit (call it i) sums the signals it receives from each of the neurons connected to it. The signal aj coming from each neighbor unit j is multiplied by the weight wij between i and j so that wij*aj models the contribution j makes to the activity of i. The sum of these activity values for each connected unit is calculated. The resulting sum might be any positive or negative number. But a neuron's activity is best modeled as a number between 0 (inactive) and 1 (maximum firing rate). So we adjust this sum so that it lies between 0 and 1 with sig, the sigmoid function : sig(n) = 1/(1+e-n). (See below for its graph.)

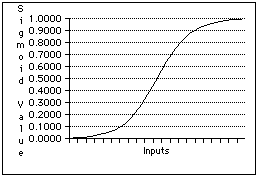
    Putting these ideas together, we can express the basic activation function for unit i in a formula.
      ai = sig(sumj wij*aj)
    This says that the activity ai of unit i is the result of multiplying the activity aj of each neighbor neuron j by the weight connecting it to i, summing these all together, and then applying the sigmoid function to this sum. Connectionists assume that all cognitive processing results from the behavior of many units all of which compute this function or a minor variant of it. Note that any possible arrangement of connections of such units can be expressed by simply setting wij to zero for any two units that are not connected. Therefore the architecture and behavior of the neural net is defined entirely by the weights between the units.

I. Connectionist Architecture

  1. Many connectionist models conform to a standard configuration called feed-forward nets. There is a bank of input units which contain the signals coming into the system, a bank of output units, recording the system's response, and usually one or more banks of hidden units that are waystations in the processing. In a connectionist model of a whole brain, the input units model the sensory neurons, the output units model the motor neurons, and the hidden units model all other neurons.
  2. The astonishing thought behind this model is that all the brain does is simply the result of massively many units calculating the activation function according to the settings of the weights (the synaptic connections).
  3. Feed-forward architectures are limited in what they can do. The signal flows directly from input to output. However we know that the brain contains recurrent pathways, that is, pathways that loop back to earlier levels. So some connectionist models have connections that loop sideways or backwards. Such models are called recurrent nets.
  4. One brand of recurrent net that Pinker describes in some detail is the autoassociator. Here the input units are fully connected. Such models do a good job at recognizing patterns.
  5. Another architecture Pinker mentions is the simple recurrent architecture used by Jordan and Elman. In simple recurrent architectures the units are not fully connected. Instead information on the hidden units is sent back to the input level, so as to provide for a kind of short term memory. Such nets have been shown to be capable of simple grammatical processing.

J. Connectionist Learning

  1. The success or failure of a neural net model depends on the selection of the right weights. But how can we determine which weights we need to accomplish a certain task? One solution to the problem is to let the net figure it out. Let the net's response to an input adjust the weights. There are two basic styles of learning in connectionist models: unsupervised, where the net simply adjusts the weights on the basis of the inputs it receives, and supervised learning where the adjustment is done on the basis of feedback from the error in the ourput. Descriptions of the most famous unsupervised (Hebbian) and supervised (Backpropagation) learning methods follows.
  2. Hebbian Learning is based on an idea of Donald Hebb. Put information at the input units, and calculate the activity of all the units. Then increase the weights between active units, and decrease those between inactive units. Do this for all the inputs that the net will encounter. This process will cause the net to classify regularities found in the input. For example, imagine that the inputs code for different features of animals: fur/feathers, 2/4 legs, forward/sideways facing eyes, sharp/blunt teeth, wings/no wings, carnivore/herbivore. Now train the net with features found in animals at the zoo. Weights between such features as carnivore, forward facing eyes, sharp teeth, will get strengthened. Also those between feathers, 2 legs and wings. The net has "discovered" the concepts "bird" and "predator". When features for a new animal are presented it will activate the units that represent the closest category to which those features belong. It is almost as if the net has extracted some prototypes from the data which it can apply to novel inputs.
  3. One of the simplest example of Hebbian learning is found in perceptrons . These models have no hidden units, so they cannot solve problems by coming up with internal representations. Although they are capable of simple classification tasks, there are many tasks (the famous xor problem for example) that they cannot do.
  4. Back-propagation (also known as error back-propagation or just backprop) is the most popular form of supervised learning. We will illustrate with the example of a net trained to pronounce English words. The spelling of a word is put on the inputs, and a code for its correct pronunciation is to be presented on the output. This task is hard because of the irregularities of English pronunciation: 'have' does not rhyme with 'came' and 'same'; 'though' does not rhyme with 'rough' oreven 'tough'. The training set will consist of a list of words together with their correct pronunciation codes. Training proceeds as follows. Start with random weights. Now present the first word in the training set, and calculate the activities of all the units. The output units will almost certainly not match the desired code for that word. For each output unit, trace the source of the error back through the network. Adjust weights (slightly) in the direction that will correct the error. Now do the same thing for the next item in the training set, and so on.

K. Connectionist Representation

  1. In local representation , single units are devoted to recording a concept. (Think grandmother neuron.)
  2. In distributed representation , the representation of an item consists of a pattern of activity across manyof the units. Nets trained with backpropagation and Hebbian learning spontaneously generate distributed representations of concepts they are learning. For example, a cluster analysis of the activation patterns on the hidden units of a NETtalk, a neural net trained to pronounce English text, shows a hierarchy of clusters and subclusters corresponding to phonetic distinctions. There is a main clustering into two: vowel, consonant. And within the consonants subclusters for voice or unvoiced, etc.. In learning the task, the network has acquired the concepts that it needs to process the inputs correctly.
  3. Distributed representations in connections models correspond to extremely complex arrays of values across many units. Therefore the representation for a concept like [cat] can code of lots of features of the concept such as mammal, pet, furry, aloof, stalks-mice, and other features (like how it looks) that we would be hard pressed to describe in language. This so called subsymbolic form of representation allows the symbol to carry its own information about what it is about. The symbol is not arbitrary and atomic the way a word in a language is. By analysing the symbol, you can find out what it "means".

L. Famous Connectionist Models

  1. Connectionist models have been used for such divergent tasks as recognizing submarines, deciding bank loans, and predicting protein folding, to name just a few. What follows are a few of the better known connectionist models trained by backpropagation.
  2. TRACE: Rummelhart and McClelland (1986)
    *Input: Phonetic code of present tense verb (sing)
    *Desired Output: Phonetic code of the past tense of that verb (sang)
    *Architecture: Feedforward net without hidden units
    *Training Set: Phonetic codes of present and past tense of 460 English verbs
    *Results: The net learned the past tenses of the 460 verbs in 200 rounds of training, and it generalized fairly well to new verbs, with good appreciation of "regularities" to be found among the irregular verbs (send / sent, build / built; blow / blew, fly / flew). During learning as the system was acquiring more regular verbs, it overregularized: (break / broked). This was corrected with more training. Children are known to exhibit the same tendency to overregularize. Whether this is a good model of how humans process verb endings is a matter of hot debate. This net does a poor job, for example, with learning the regular ending rule for novel verbs.
  3. NETtalk: Sejnowski and Rosenberg (1987)
    *Input: 7 letters of the text (including space) in a moving window
    *Desired Output: Phonetic code for the center few letters, which is sent to a speech synthesizer
    *Architecture: Standard 3 layer feed-forward net. (80 hidden units)
    *Learning: A large training set of text coupled with its phonetic transcription.
    *Results: During learning the system goes through stages of babbling, double-talk, and finally intelligible speech, (with some accent). Generalization to novel text is good. Statistical analysis shows that hidden units use a distributed representation of basic phonological features.
  4. Elman's work
    * Input: Words drawn from a small set of English words (23 words plus space) coded in 1s and 0s.
    * Output: One output unit for each each word in the set.
    * Architecture: Simple Recurrent Net  
    *Training Set: Grammatical sentences of from this vocabulary for a brand of English restricted to a small subset of its grammatical rules. The grammar did, however, provide for a hard test of grammatical awareness: subject-verb agreement across arbitrarily long relative clauses:
    Any man who hates women who hate men .. also hates feminists.
    *Desired Output: When a word from the sentence is applied to inputs, the desired output is the next word in the sentence. (Of course the net can't possibly succeed at this task.)
    *Results: Nets were trained to be extremely accurate in the following sense, on the presentation of a sequence of words, all and only words that would be legal continuations at that point are active beyond a certain threshold at the output. When a word is presented that violates the rules of grammar no words reach threshold at the output. The trained net came very close to this desired performance.


M. Attractions of Connectionist Models

  1. Biological Plausibility. Neural net models "look like" the processing that we find in a brain, especially when we look at the processing we know about: sensory input and motor output. There is evidence for Hebbian learning at synapses. The brain's processing, unlike the usual classical computers, which are serial and fast, is highly parallel and rather slow.
  2. Fuzziness and Soft Constraints. Nets can learn to appreciate subtle statistical patterns that would be very hard to express as hard and fast rules. This fuzziness allows them to avoid the brittle and overly literal behavior displayed by classical models.
  3. Fast Processing of Multiple Constraints . Nets can quickly resolve in parallel acomplex set of conflicting forces to make a decision.
  4. Graceful Degradation . When units are lost, the net behaves almost as well. In classical systems the loss of a circuit typically causes a fatal processing error.
  5. Flexible Response to Noise. When the inputs are noisy (if part of the input is inaccurate or obscured by some other signal) nets respond appropriately (though somewhat less accurately).
  6. Vector Representation . There is evidence that the brain is deeply committed to representations in the form of vectors (arrays of values). For example, coding for color and taste are both by vectors of 3 and 4 values. Neural net architectures are perfectly designed to handle vector processing.
  7. Unified Theory of Learning. Classical accounts employ a variety of different learning techniques. Connectionists have a simple and fairly unified theory of learning based on backpropagation and Hebbian processes. Their models spontaneously learn, often in ways the resemble animal and human learning.

N. Weaknesses of Connectionist Models

  1. Biological Implausibility
    Simplicity. Neural nets are too simple to capture the brain's processing. For example, they leave out neuro-transmitters, and the spikiness of neural firing.
    Backward Connections. Backpropagation requires signals be sent both forward and backward in a neural net. But there seem to be few if any backward neural connections. (However, if units represent groups of neurons, the backward pathways are compatible with what we know about neurology.)
    Slow learning. Connectionist learning is slow, requiring hundreds of thousands of presentations. But people learn some things from a single example.
  2. Processing Limitations
    Uniqueness. If things are represented by their features, as is often done in popular connectionist models, you can not represent the difference between two things that have the same features. You can't express distinctness of individuals properly. Pinker relates this failing to the problems with the historical doctrine of associationism , the idea that all mental processing can be done by associating ideas one to another. In such a scheme it is truly difficult to capture the idea of uniqueness of an individual. In response to Pinker, Garson noted that not all models must represent things with features only; it is possible to create connectionist models that respect uniqueness.
    Compositionality. It would seem that symbolic processing is required to carry out certain kinds of reasoning operations. For example, to reason generally from A&B to A, I need to represent A&B as containing A, &, and B, so that I can drop off the A part. This suggests that at some level or other the brain must represent the constituents A, &, and B of A&B, and apply a rule that is sensitive to these parts. (In this case the rule would be: take the left part and drop the others.) Classical computers have an easy time of this, but it is not clear that connectionist models can do so without already implementing the representations and rules strategy. The strategy of just making up a separate representation for each and every instance of reasoning from A & B to A would be way too costly. Radical connectionists, who believe they can explain cognition without classical structures, may face serious problems in explaining compositionality. I should note however, that the issue of whether connectionist models (especially recurrent ones) can handle compositional processing without being classical processors is a matter of hot debate.
    Binding. A related complaint is that neural nets are not very good at binding one concept to another: For example: in 'John loves Mary' 'John' is bound to the subject role and 'Mary' to the object role. Simple connectionist architectures have trouble separating out information about (for example) the subject, from the object. All the net can do is associate 'John' with 'loves' and 'loves' with 'Mary'. The trouble with association is that it is a "two way street". Once 'loves' is associated with 'Mary', 'Mary 'is associated with 'loves', and there is potential confusion with the sentence 'Mary loves John'. So if you say John loves Mary and then that Mary hates John, the idea that John is the lover and the recipient of Mary's hate might get confused with the idea that Mary is the lover and John the person hated. What is needed is a way to bind objects like John and Mary to their respective roles.
    Recursion. Humans can understand sentences of unlimitedly long length. Consider: 'John fed the dog that ate the cat that ate the rat that ate the spider that ate.....that lived in the house that Jack buildt'. Symbolic processors can handle this repetition of subunits (or recursion ). Pinker claims that connectionist models cannot do so without implementing classical machines. Garson notes that this is still a matter of some debate.
    Non-Fuzziness. Connectionist models handle fuzziness in concepts well. But there are important occasions where human abilities depend on drawing strict boundaries between things and applying clear cut rules. (You can't be a little bit married, or a little bit pregnant.) Simple connectionist models have trouble with this. Garson noted that some of the difficulties can be handled with recurrent neural nets.
    Poor Generalization. Sometimes connectionist models do not generalize to novel cases the way humans do. For example, when NETtalk is given such odd and nonsense verbs as 'biznack', it does asnwer as English speakers do: biznacked. So the net does not seem to generalize properly to what we all know about past tense formation: when in doubt add 'ed'. What the model lacks is the appreciation of a rule, which suggests that only classical models can handle this problem properly. Again the matter is a topic of hot debate.


O. Useful Website on Connectionism.